Über die Messung mit Drehtisch habe ich im letzten Post bereits geschrieben. Dabei bin ich auf Vor- und Nachteile eines Drehtisches für die Zahnradmessung eingegangen und wie wichtig die Einmessung des Drehtisches ist.
Gehen wir davon aus, dass Sie sich für einen Drehtisch entschieden haben bzw. mit ihrem Verzahnungsmessgerät immer mit Drehtisch messen. Sie als Messtechniker sind für die Korrektheit Ihrer Messergebnisse verantwortlich. Der Betriebsleiter verlässt sich darauf, da die Fertigungssteuerung auf Basis Ihrer Daten reagiert. Entweder wird weiter produziert oder die Maschinen werden gestoppt.
Wie stellen Sie also sicher, dass Sie verlässliche und stabile Messergebnisse liefern?
Heute schauen wir uns an, welchen Einfluss der Drehtisch auf die Messergebnisse haben kann und worauf Sie achten müssen.

Messstrategie
Die Drehtischeinmessung basiert auf den Kugelmessungen. Solange diese Ergebnisse stabil sind, ist alles in Ordnung. Was also kann zu unsicheren Ergebnissen führen? – Die stabile Befestigung der Einmesskugel auf dem Drehtisch setze ich voraus. Genauso wichtig – aber nicht so offensichtlich – ist die Messstrategie.
Sinnvollerweise misst man die Kugel möglichst vollständig, d.h. in mehreren Schnitten, die über 360° geführt werden.
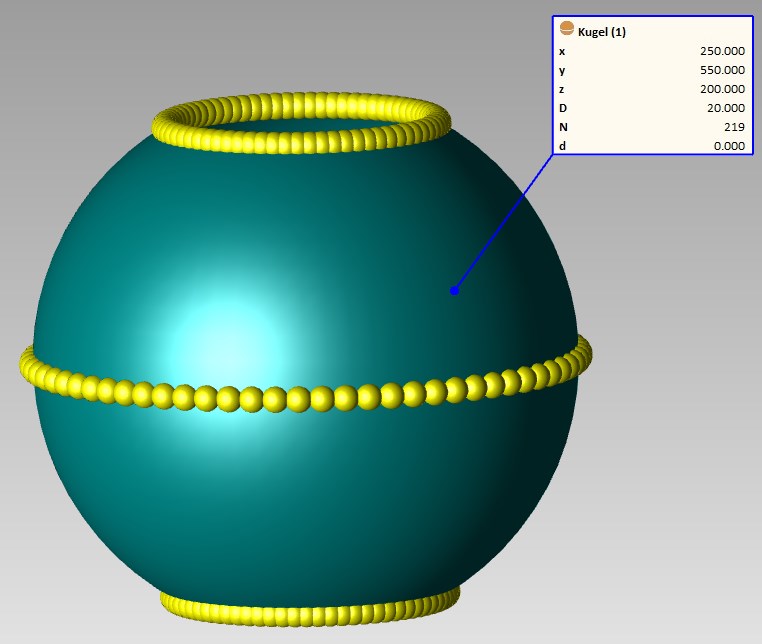
Da die Drehtischeinmessung regelmäßig wiederholt werden muss, ist man bestrebt, die Dauer der Einmessung möglichst kurz zu halten. Deshalb wird sie häufig auf die Messung eines Kreises am Äquator und eines Punktes am Pol reduziert. Das ist bezogen auf die Güte der Einmessung kein Problem aufgrund der geringen Abweichungen der Einmesskugel (Formfehler <= 0.001 mm) führt auch diese Messung zu zuverlässigen Ergebnissen.
Wichtig bleibt bei der Kreismessung, dass der Kreis im Idealfall über volle 360° gemessen wird. Warum? Die Messunsicherheit steigt deutlich an, je kleiner der Kreisausschnitt ist, über den der Kreis gemessen wird. Dazu hat Dr.-Ing. Michael Hernla eine Untersuchung durchgeführt, die Sie unter dem folgenden Link studieren können Dr.-Ing. Michael Hernla: „Messstrategien am Kreis und am Kreisausschnitt“. Lassen Sie uns das an einem Beispiel anschauen:
Beispiel: Kugelmessung über verschiedene Kreisausschnitte
Die Untersuchung von Herrn Hernla zeigt, dass die Messunsicherheit einer Kreismessung deutlich ansteigt, wenn der gemessene Ausschnitt weniger als 180° ist. Je kleiner der Kreisausschnitt, umso größer die Messunsicherheit.
In unserem Beispiel messen wir eine Kugel. Die Kugel wird mittels eines Kreises am Äquator und einem Punkt am Pol gemessen. Dadurch haben wir eine vergleichbare Konstellation wie bei der o.g. Kreismessung. Wir werden sehen, dass die Messunsicherheit der Kreismessung das Ergebnis der Kugelmessung entsprechend beeinflusst.
Randbedingungen
Die Kugel (Durchmesser = 20.0 mm) wird mittels eines Kreises und eines Punktes am Pol gemessen (s.o.). Während des Tests wird der Kreisausschnitt variiert: 360°, 180°, 120°, um dessen Einfluss auf das Messergebnis der Kugel zu ermitteln. Die Messpunkte sind virtuell. Jedoch sind diese idealen Punkte mit einem Rauschen beaufschlagt. Dadurch ergeben sich realistischere Verhältnisse, da bei einer realen Messung die Messdaten ebenfalls immer „verrauscht“ sind (z.B. durch Vibrationen, Steuerung des Messgerätes, Formfehler des Werkstücks). Alle drei Tests verwenden identische Messdaten, bei den Kreissausschnitten von 180° und 120° jedoch jeweils nur einen entsprechend reduzierten Anteil der Daten.
Das erwartete Ergebnis ist
- Kugeldurchmesser: D = 20.000 mm
- Position: X = 0.000 mm, Y = 0.000 mm, Z=200.000 mm
- Formfehler: d = 0.035 mm (bedingt durch das überlagerte Rauschen)
Anmerkung: Aus didaktischen Gründen habe ich bewusst ein etwas größeres Rauschen verwendet, damit die Auswirkungen deutlich sichtbar sind.
Messung über 360°
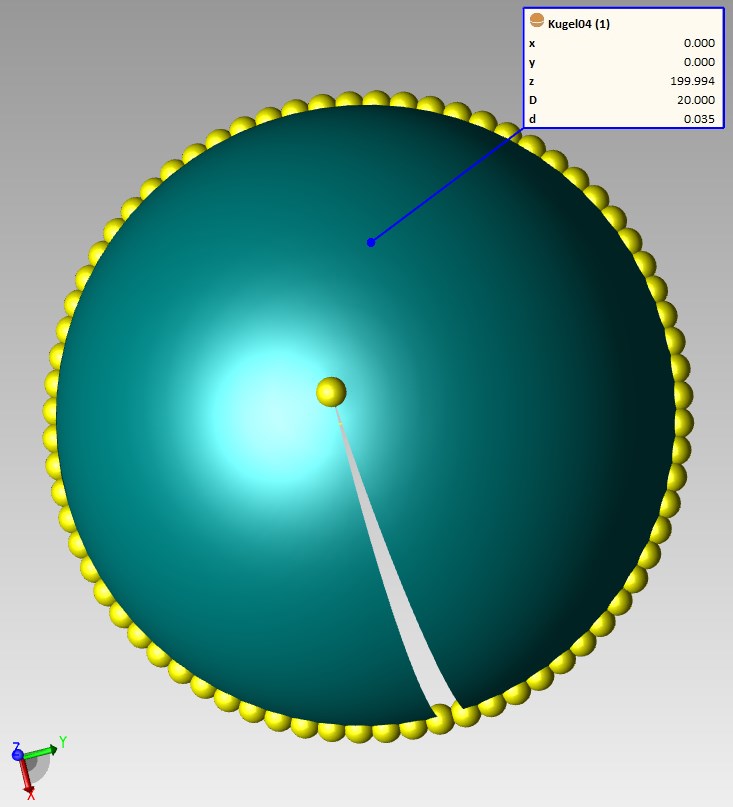
Bei der Messung über 360° sind die Messergebnisse quasi noch ideal. Die einzige Abweichung, die auffällt, ist die Position in Z. Diese wird durch ein Verrauschen des Punktes am Pol verursacht. Dies macht deutlich wieviel Einfluss dieser eine Punkt auf die Z-Komponente hat.
Messung über 180°
Für diesen zweiten Test werden die identischen Messpunkte wie bei der Messung über 360° verwendet, jedoch nur die halbe Punktzahl. Gut erkennbar ist das an dem Wert d = 0.035 mm, der für beide Messungen identisch ist. Es handelt sich hierbei um die Differenz zwischen der größten und der kleinsten Abweichung von der idealen Form der berechneten Kugel. „d“ ist identisch mit der Rundheitsabweichung.
Warum ist die Rundheitsabweichung bei 180° genauso groß wie bei 360°? Bei dem Rauschen handelt es sich um eine regelmäßige Störung (Sinus- bzw. Cosinus-Schwingung). Das Rauschen enthält keinen „Peak“, der nur an einer bestimmten Stelle auftritt und dadurch das Ergebnis maßgeblich beeinflusst.
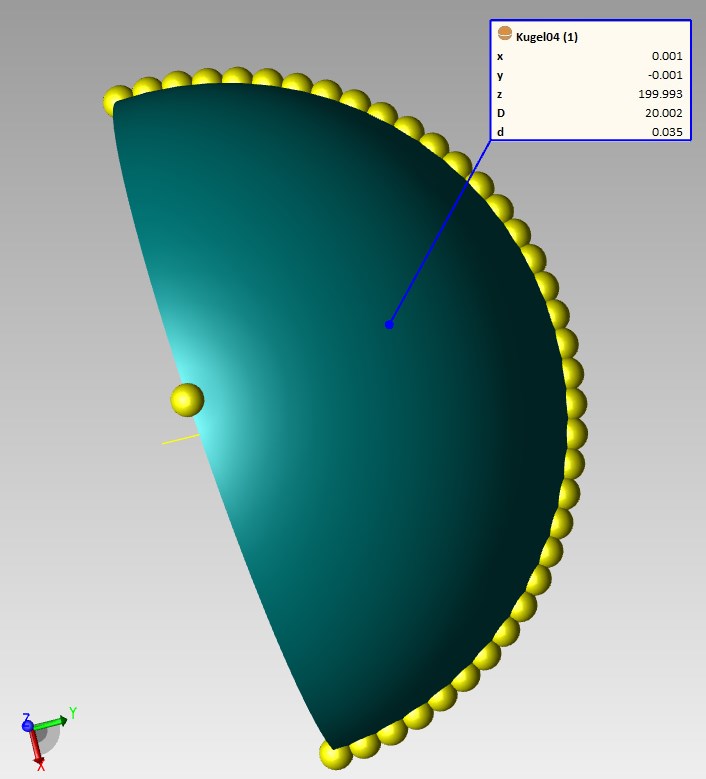
Bei der Messung über 180° erkennt man erste Abweichungen in den Messergebnissen. Die Position in X- und Y-Richtung ist leicht verschoben. Der Durchmesser hat sich um zwei Mikrometer verändert. Die Abweichungen sind vorhanden, sind aber noch klein. Mit zwei Mikrometer könnte man sagen, sie liegen noch Bereich der Maschinengenauigkeit.
Messung über 120°
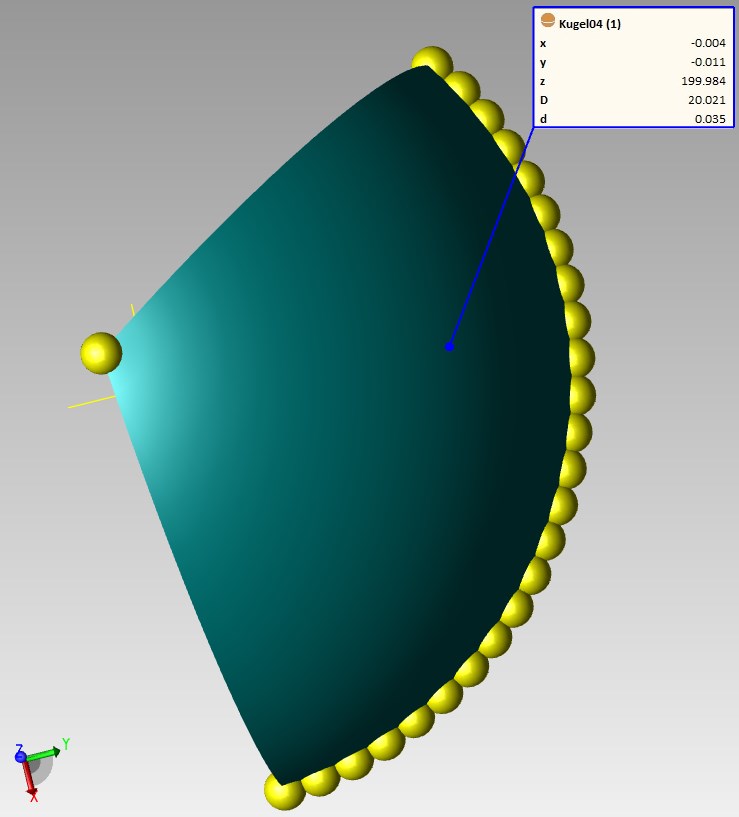
Kugelmessung über 120°: deutliche Abweichung der Position und des Durchmessers aufgrund des reduzierten Messbereichs und der vorhandenen Formabweichungen (Rundheit=0.035 mm)
Die Messung über 120° zeigt deutliche Abweichungen. Die Position weicht in Y-Richtung um 0.011 mm ab. Die Z-Richtung mittlerweile um 0.016 mm. Hier liegt die große Abweichung nicht an dem Punkt auf dem Pol. Dieser ist immer noch an der gleichen Stelle wie bei der Messung über 360°. Das Problem ist, dass sich durch den kleinen Kreisausscchnitt der Durchmesser nicht mehr sicher berechnen lässt. Der ermittelte Durchmesser liegt jetzt bei 20.021 mm. Das zeigt am deutlichsten die Problematik. Die Kugel hat sich während der Messung nicht verändert. Die eingeschränkten Messdaten führen dazu, dass Durchmesser und Position der Kugel nicht mehr sicher bestimmt werden können.
Wenn Sie an dieser Stelle – Einmessung des Drehtisches = Basis Ihrer kompletten Verzahnungsmessung! – Abweichungen von über 20 Mikrometer haben, können Sie sich vorstellen, was dies für Auswirkung auf das eigentliche Messergebnis der Verzahnungsmessung hat. Ihnen werden an der Verzahnung Abweichungen aufgezeigt, die überhaupt nicht vorhanden sind.
Fazit
Die o.g. Beispiele zeigen sehr deutlich wie sich die ermittelten Werte für den Durchmesser und die Position verändern. Die Messunsicherheit steigt mit kleiner werdendem Kreisausschnitt deutlich an. Bei einem Kreisausschnitt von nur noch 120° unterscheiden sich Solldurchmesser (= 20.000 mm) und Istdurchmesser (= 20.021 mm) um mehr als 20 Mikrometer und das, obwohl wir bei allen drei Messungen identische Messpunkte verwendet haben. Abweichungen in dieser Größenordnung sind verheerend für die Verzahnungsmessung. Das gilt vor allem wenn diese Abweichungen bei der Drehtischeinmessung auftreten, die die Grundlage für die gesamte Messung ist.

