Kratzen Sie sich gerade am Kopf und fragen sich, was diese seltsame Frage soll? – Gut so, dann habe ich Ihre Aufmerksamkeit geweckt.
Die Frage ist durchaus berechtigt. Ich habe sie jedoch absichtlich zweideutig formuliert, damit man sich wundert. Wenn Sie sich als deutschsprechender Leser schon wundern, was meinen Sie, wie es den Lesern geht, die der deutschen Sprache nicht mächtig sind. Diese lassen sich den Artikel automatisch auf Englisch übersetzen und verstehen nur noch „Bahnhof“.

Die eigentliche Frage lautet: Gibt es an einem Zahnrad nur den einen Schrägungswinkel oder gibt es mehrere Schrägungswinkel?
Einer oder mehrere?
Die alten Hasen der Zahnradtechnik wissen natürlich Bescheid. Die anderen meinen zu wissen, dass es nur einen Schrägungswinkel an einem Zahnrad gibt. Über diesen ist schließlich die Geometrie der Verzahnung definiert: Teilkreis- und Grundkreisdurchmesser hängen von diesem Winkel ab.
Die richtige Antwort ist: Eine Verzahnung hat mehr als einen Schrägungswinkel!
Der Schrägungswinkel ist vom Durchmesser abhängig, auf dem er definiert ist. Deshalb gibt es an einer Schrägverzahnung unendlich viele Schrägungswinkel. An einer Geradverzahnung ist der Schrägungswinkel egal auf welchem Durchmesser immer null.
Der Schrägungswinkel, der auf der Zeichnung oder im Datenblatt angegeben wird, ist ein spezieller Schrägungswinkel. Es ist der Schrägungswinkel auf dem Teilkreisdurchmesser.
Angabe des Schrägungswinkels
Zu der Angabe des Schrägungswinkels (Formelzeichen: β) gehört eigentlich die Angabe des Durchmessers, auf dem er sich befindet. Die allgemeine Bezeichnung ist:
Schrägungswinkel βy = … auf Durchmesser dy = …
Das „y“ steht für einen beliebigen Durchmesser. Um Schrägungswinkel auf verschiedenen Durchmessern zu unterscheiden, kann man als Indize eine Zahl angeben: β1 =… auf d1=…, β2=… auf d2 = …, usw.
Ausnahmen
Von dieser allgemeinen Angabe gibt es zwei Ausnahmen.
Schrägungswinkel auf dem Grundkreisdurchmesser
Der Schrägungswinkel auf dem Grundkreisdurchmesser wird als Grundschrägungswinkel mit dem Formelzeichen βb angegeben. Dadurch ist die zusätzliche Angabe des Durchmessers als Zahlenwert nicht notwendig.
Schrägungswinkel auf dem Teilkreisdurchmesser
Wird für den Schrägungswinkel β kein Durchmesser angegeben, dann handelt es sich um den Schrägungswinkel auf dem Teilkreisdurchmesser. Dies ist eine Konvention, die so auch in den gängigen Verzahnungsnormen verwendet wird. Dieser Schrägungswinkel wird für die Berechnung von Teilkreisdurchmesser und Grundkreisdurchmesser verwendet.
Warum verschiedene Schrägungswinkel?
Kommen wir zu der interessanten Frage: Warum haben wir verschiedene Schrägungswinkel an einer Verzahnung?
Zahnrad – Schnecke – Schraube
Um das zu erklären, muss ich etwas ausholen. Bei einer Schrägverzahnung wendeln sich die Zähne um das Zahnrad herum. Ist die Zahnbreite groß genug, würden sich die Zähne über 360° wendeln, d.h. einmal komplett um das Zahnrad herum. Bei einem Stirnrad sieht man das eher nicht, dafür aber bei einer Schnecke. Man kann die Zylinderschnecke als Sonderfall einer Schrägverzahnung ansehen. Ich erwähne die Zylinderschnecke an dieser Stelle absichtlich, da sie von der Geometrie dem Gewinde einer Schraube ähnelt (s. Bild). Deshalb verwendet man bei der Schnecke den Steigungswinkel anstatt dem Schrägungswinkel. Beide Winkel stehen in Bezug zu einander:
Steigungswinkel = 90° – Schrägungswinkel

Bei einem Gewinde und bei einer Schnecke ist es üblich, dass sich die Zähne bzw. Gewindegänge mehr als einmal um den Grundkörper herumwinden.
Die Steigung
Windet sich ein Zahn (Gewindegang) um 360° herum, dann wird in Abhängigkeit vom Steigungswinkel über diese eine Umdrehung eine Höhe zurückgelegt. Diese Höhe wird bei einer Schnecke als Steigungshöhe und bei einem Gewinde als Gewindesteigung bezeichnet.
Bei einem Schraubengewinde ist dieser Sachverhalt für jeden klar. Deshalb habe ich diese Parallele gezogen. Wir müssen jetzt aber einen Schritt weitergehen und diesen Zusammenhang verbildlichen.
Abwicklung
Das Bild wird einfacher, wenn wir vom 3-dimensionalen zum 2-dimensionalen wechseln. Wie machen wir das? Wir wickeln den Gewindegang (bzw. den Zahn) ab. Das heißt, wir stellen uns vor, dass wir den zylinderförmigen Körßer der Schraube (des Zahnrad) der Länge nach aufschneiden und. Ein Beispiel einer Zylinder-Abwicklung finden Sie in Wikipedia. An einer Schrägverzahnung sie die Abwicklung eines Zahnes so aus:
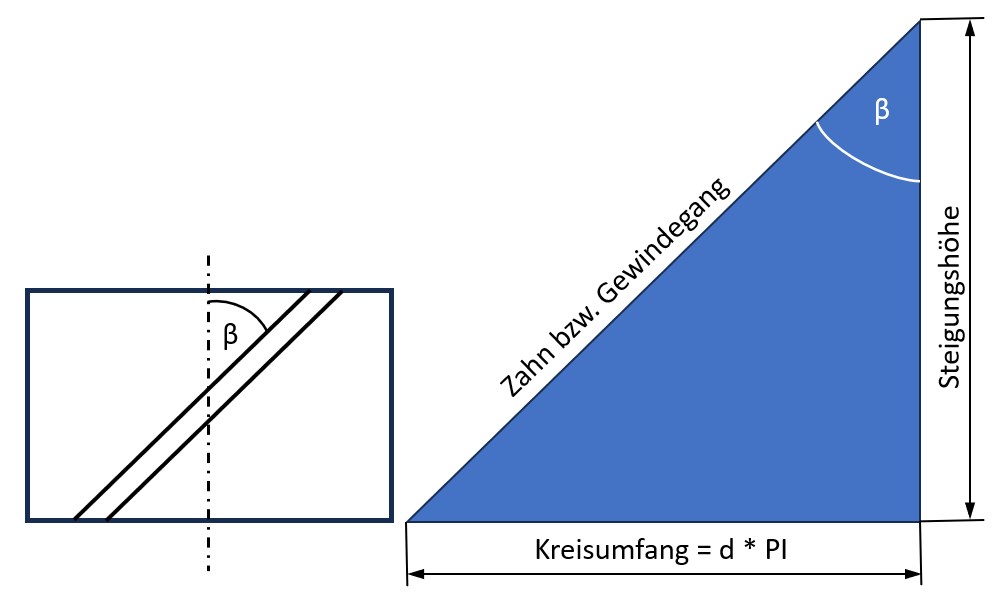
Das blaue Dreieck zeigt den abgewickelten Zahn. Der Zahn ist über 360° abgewickelt, dadurch entspricht die Abwicklungslänge dem Kreisumfang und die Höhe des Dreiecks der Steigungshöhe. Der Schrägungswinkel ist am Zahnrad und am Dreieck eingezeichnet, beide sind identisch. Das Bild zeigt die allgemeinen Zusammenhänge: Die Steigungshöhe hängt demnach vom Schrägungswinkel und vom Kreisumfang ab.
Bei einer Schrägverzahnung ist die Zahnform und die Zahndicke konstant über die Zahnbreite. Das heißt der Zahn verändert sich nicht entlang der Zahnradachse. Vor dieser Voraussetzung ist es klar, dass die Steigungshöhe auf jedem Durchmesser identisch sein muss. Wäre dies nicht der Fall, dann würden sich Zahnform und Zahndicke verändern.
Fall #1: Schrägungswinkel ändert sich mit dem Durchmesser
Dies ist der Normalfall. Der Schrägungswinkel muss sich mit dem Durchmesser ändern, damit die Steigungshöhe über alle Durchmesser konstant ist.
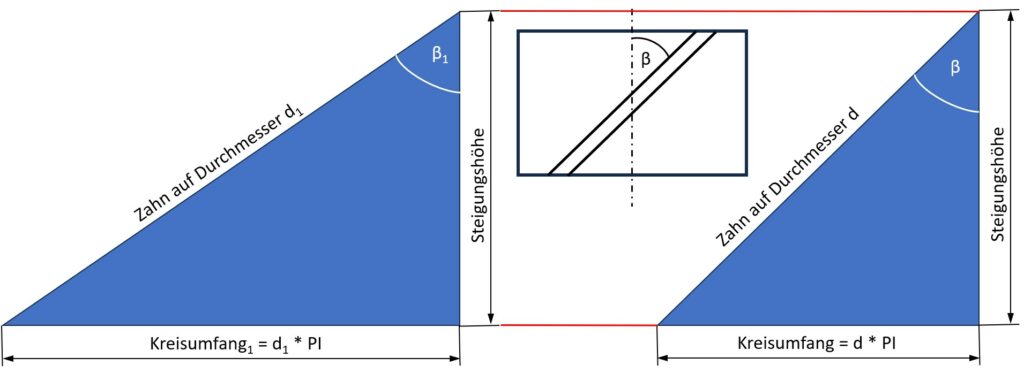
Das obige Bild macht den Zusammenhang deutlich. Die blauen Dreiecke zeigen den abgewickelten Zahn auf zwei verschiedenen Durchmessern.
Das rechte Dreieck zeigt den Zusammenhang am Teilkreisdurchmesser (= d), mit dem Schrägungswinkel am Teilkreis so wie er in der Zeichnung angegeben ist.
Das linke Dreieck zeigt den Zusammenhang auf einem Durchmesser d1, der größer ist als der Teilkreisdurchmesser. Dadurch vergrößert sich der Kreisumfang. Um eine konstante Steigungshöhe auf beiden Durchmessern zu erhalten, muss der Schrägungswinkel β1 größer sein als der Schrägungswinkel β auf dem Teilkreisdurchmesser.
Fall #2: Identischer Schrägungswinkel über alle Durchmesser
Anmerkung: Fall #2 entspricht nicht der Realität. ist ein Er ist ein Was-Wäre-Wenn-Szenario. Er soll nur verdeutlichen, was in diesem Fall passieren würde.
Wäre der Schrägungswinkel konstant und damit auf jedem Durchmesser identisch, würde sich die Steigungshöhe ändern.
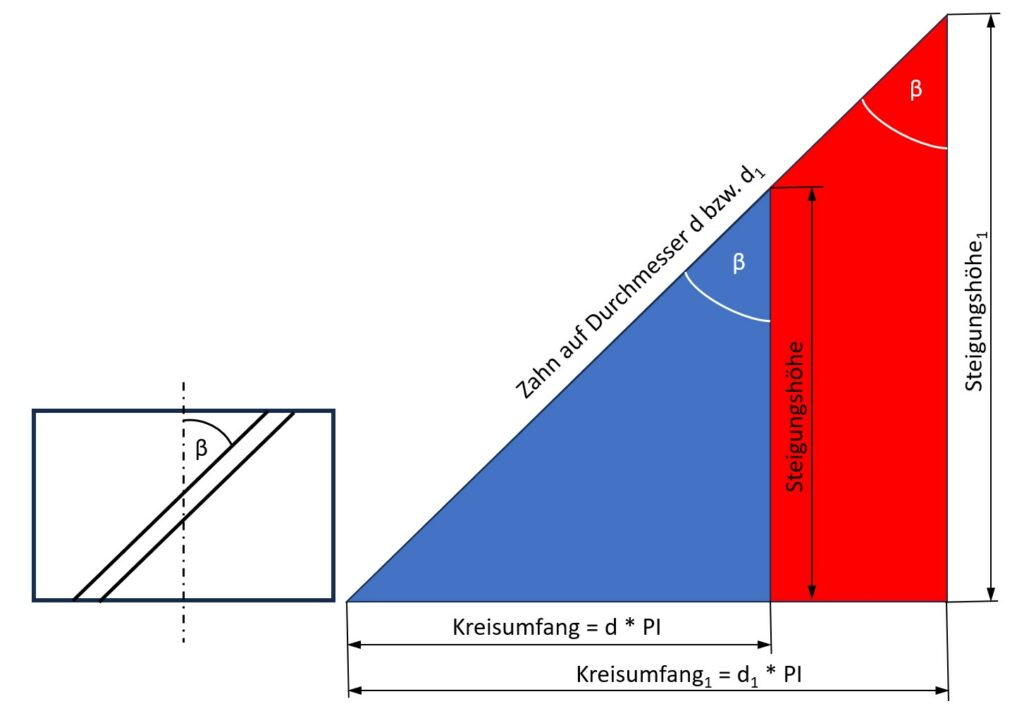
Warum ist das so? Das Dreieck in der obigen Abbildung zeigt den Zusammenhang zwischen dem Schrägungswinkel, der Steigungshöhe und dem Kreisumfang. Dieses Bild zeigt den abgewickelten Zahn (blaues und rotes Dreieck) für zwei verschiedene Durchmesser: d und d1. Der Schrägungswinkel ist für beide Durchmesser identisch. Der Kreisumfang ändert sich mit dem Durchmesser (Umfang = Durchmesser * PI). Dadurch dass der Schrägungswinkel konstant ist, muss sich folglich die Steigungshöhe ändern.
Bei einer 360°-Umdrehung würde die Flanke auf Durchmesser d1 einen größeren Weg entlang der Zahnradachese zurücklegen. Das hätte zur Folge, dass sich der Zahn verzerrt, während er sich um das Zahnrad herumwendelt.
Fazit
Bei einer Schrägverzahnung gibt es mehr als einen Schrägungswinkel. Der Schrägungswinkel ändert sich mit dem Durchmesser. Hintergrund dafür ist, dass die Steigung auf jedem Durchmesser identisch sein muss. Nur so bleiben Zahnform und Zahndicke über die Zahnbreite identisch.
Bei einer Geradverzahnung ist der Schrägungswinkel gleich null. In diesem Fall ist der Schrägungswinkel unabhängig vom Durchmesser. Es gibt hier tatsächlich nur einen Schrägungswinkel.
