Die Kopf- und Fußkreismessung ist nicht Bestandteil einer Standard-Verzahnungsmessung. Trotzdem wird sie häufig bei der Verzahnungsmessung mit durchgeführt. Das liegt daran, dass Kopf- und Fußkreis auf der Zeichnung toleriert sind und die Maße dementsprechend überprüft werden müssen.
Es handelt sich dabei nur um die Messung und Auswertung von Kreisen. Dies ist eine Standardmessaufgabe in der Koordinatenmesstechnik und könnte deshalb unabhängig von der Verzahnungsmessung erfolgen. Es ist jedoch von Vorteil, diese Messung von der Verzahnungsmesssoftware durchführen zu lassen.
Die Messung des Kopfkreises ist noch relativ einfach zu programmieren. Dahingegen stellt die Fußkreismessung aufgrund der Messung in den Zahnlücken höhere Anforderungen an das Messprogramm. Der Vorteil der Verzahnungsmesssoftware ist, dass diese den kollisionsfreien Messablauf automatisch erstellt.
Bei einer vollständigen Verzahnung reicht es in der Regel aus, Punkte an vier Zähnen gleichmäßig verteilt über den Umfang aufzunehmen. Dafür verwendet man meist die Zähne/Zahnlücken, an denen auch die Profil- und Flankenlinienmessung durchgeführt wird. Aus den Messpunkten wird der jeweilige Kreis berechnet. Dies erfolgt über gängige Berechnungsalgorithmen wie das Ausgleichsverfahren nach Gauß (= Gaußkreis).

Segment-Verzahnung
Eine Segment-Verzahnung ist eine Verzahnung, bei der Zähne fehlen, z.B. hat die vollständige Verzahnung 24 Zähne, es sind jedoch nur 23 Zähne vorhanden.

Bei einer Segment-Verzahnung geht man im Allgemeinen genauso vor. Es gibt jedoch bestimmte Segment-Verzahnungen, bei denen das o.g. Vorgehen zu Problemen führen kann. Dies sind Segmente, bei denen auf weniger als 180° des Umfangs Zähne vorhanden sind.

Was ist an diesen Verzahnungen problematisch?
Nehmen wir als Beispiel eine Segment-Verzahnung mit z=58 (Zähne der vollständigen Verzahnung) und z_s = 17 (vorhandene Zähne = Zähne des Segments).
Die Verzahnungsmessung läuft problemlos durch, die Auswertung und Protokollierung funktionieren ebenfalls problemlos. Ein Blick in das Messprotokoll lässt uns stutzen:

Die ermittelten Durchmesser für Kopfkreis und Fußkreis sind deutlich zu groß! Die Verzahnung ist eigentlich maßhaltig. Sie ist auch im eingebauten Zustand nicht auffällig. Diese Ergebnisse erscheinen fragwürdig. Deshalb ein Blick auf die Einzelwerte der Kopf-/Fußkreismessung:
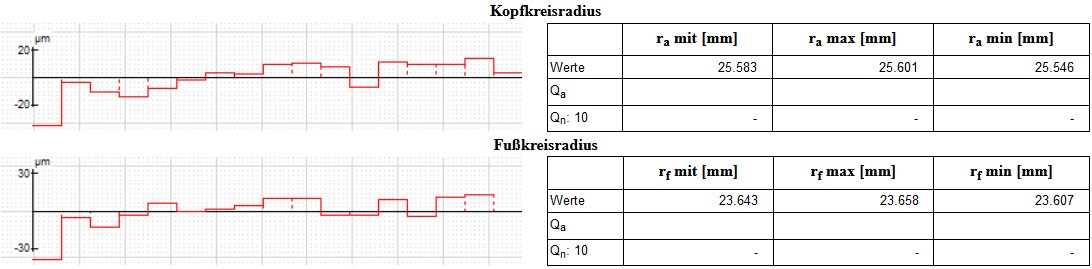
Die Diagramme zeigen keine Auffälligkeiten. Die Anzahl der der Werte ist ebenfalls i.O.:
- Kopfkreisradius: 17 Werte
- Fußkreisradius: 16 Werte
Da es sich um ein Segment handelt, ist eine Zahnlücke weniger vorhanden.
Die Ursache
Die Ursache für die großen Werte für die Durchmesser sind nicht die Messwerte, sondern die Auswertung.
Ausgleichsverfahren
Die o.g. Durchmesser sind über die Auswertung als Gauß-Kreis ermittelt worden. Die Gauß-Berechnung (= Summe der kleinsten Fehlerquadrate) führt zu einem Kreis, der „bestmöglich in der Mitte zwischen allen Messpunkten liegt (vgl. AUKOM ). Diese Berechnung führt zu stabilen Ergebnissen, da sie unempfindlich gegenüber Ausreißern ist. Die Hüllkreis-Berechnung führt zu einem Kreis, bei dem alle Messpunkte innerhalb des Kreises liegen. Der Durchmesser soll dabei so klein wie möglich sein. Ausreißer in den Messpunkten können das Ergebnis der Hüllkreis-Berechnung deutlich beeinflussen.
Außermittigkeit
Da wir die Gauß-Berechnung verwendet haben, wäre der Einfluss möglicher Ausreißer gering.
Die Diagramme für Kopf- und Fußkreisradien zeigen zwar kleinere Werte am Anfang des Segments. Diese können durch eine etwaige Außermittigkeit der Verzahnung verursacht sein. Eine Außermittigkeit wirkt sich auf radiale Werte aus, jedoch nicht auf Durchmesserwerte. Deshalb können wir dies als Ursache ebenfalls ausschließen.
Das eigentliche Problem
Das eigentliche Problem ist die Anzahl der vorhandenen Zähne. Die Segment-Verzahnung hat nur 17 Zähne. Im Vergleich zu 58 Zähnen für die vollständige Verzahnung. Es sind also auf 17/59 = 0,288 -> weniger als 1/3 der vollständigen Verzahnung Zähne vorhanden. Folglich sind nur auf einem Bereich von ca. 104° Zähne und damit Messwerte vorhanden!
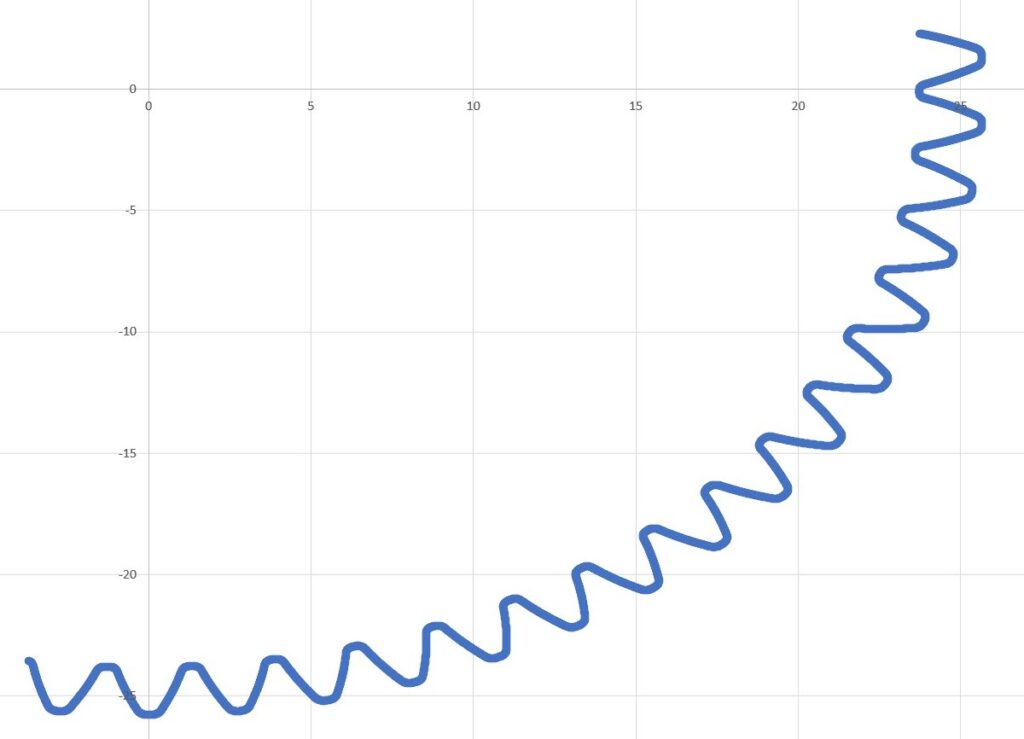
Das ist für die Berechnung eines Kreises – egal ob als Gauß- oder als Hüllkreis – problematisch. Untersuchungen haben gezeigt, dass die Messunsicherheit bei der Kreismessung von diesen Faktoren abhängt:
- Größe der Formabweichung,
- Messpunktanzahl,
- Zentriwinkel des Kreisausschnitts
Je größer die Formabweichung ists, umso größer ist die Messunsicherheit. Je geringer die Messpunktanzahl ist, umso größer ist die Messunsicherheit. Je kleiner der Kreissausschnitt, der gemessen wird, umso größer ist die Messunsicherheit. Wobei die Messunsicherheit stark ansteigt, wenn der Kreis auf weniger als 180° gemessen wurde (vgl. Hernla: „Messstrategien am Kreis und am Kreisausschnitt“).
Dr.-Ing. Hernla führt aus, dass sich die Messunsicherheit für den berechneten Durchmesser um den Faktor = 24 erhöht, wenn man nur über 60° misst anstatt über 360°. Bei der Messung eines Kreisausschnittes von nur 6° ergibt sich ein Faktor = 1000.
In unserem Beispiel (Kreisausschnitt = 104°) würde sich die Messunsicherheit für den Kreisdurchmesser nur um den Faktor = 7 erhöhen.
Die Lösung
Das stellt uns vor ein Problem. Wir können bei unserer Messaufgabe weder die Messpunktanzahl erhöhen, noch den Kreisausschnitt vergrößern, auf dem wir messen. Da wir die Messtrategie nicht verändern können, können wir nur die Art der Auswertung ändern.
Das Auswerteverfahren für einen Gauß- oder Hüllkreis will aus den beschränkten Messinformationen einen vollständigen Kreis berechnen. Eine andere Möglichkeit ist, aus den vorhandenen Radiuswerten einen Durchmesser zu berechnen. Dafür berechnet man zunächst den mittleren Radius. Der mittlere Radius wird über das Multiplizieren mit zwei auf den Durchmesser hochgerechnet. Das Ergebnis (s.u.) unterscheidet sich deutlich zu der Berechnung nach Gauß (Differenz ca. 0,160 mm!)

Dieses Verfahren klingt etwas hemdsärmelig, da die Durchmesserberechnung stark vereinfach ist. Die Erfahrung zeigt jedoch, dass dies für Segment-Verzahnungen mit Zähnen auf weniger als 180° zu genaueren Ergebnissen führt als die Auswertung als Gauß- oder Hüllkreis.

